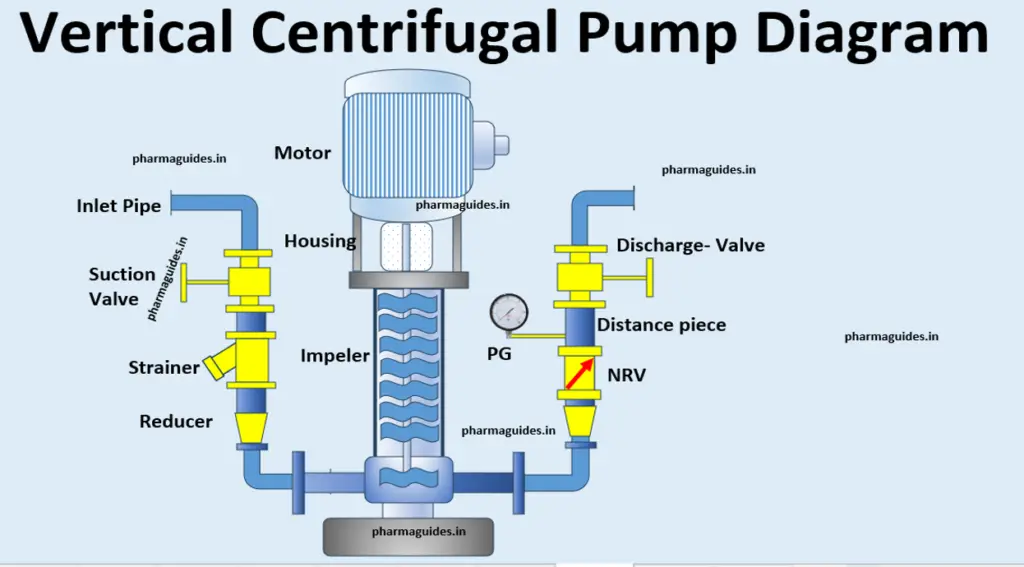
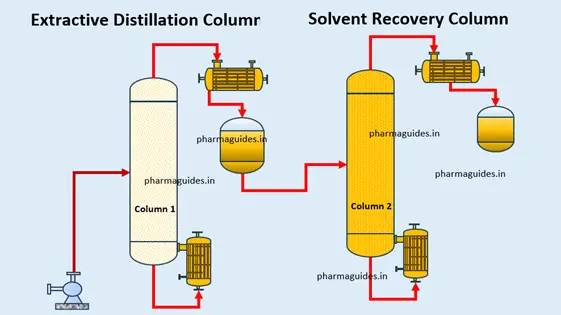
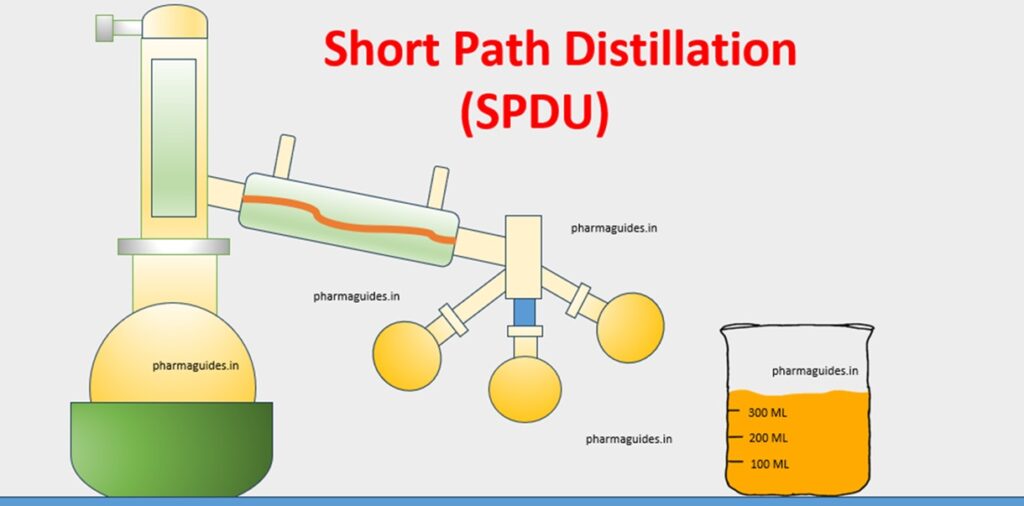
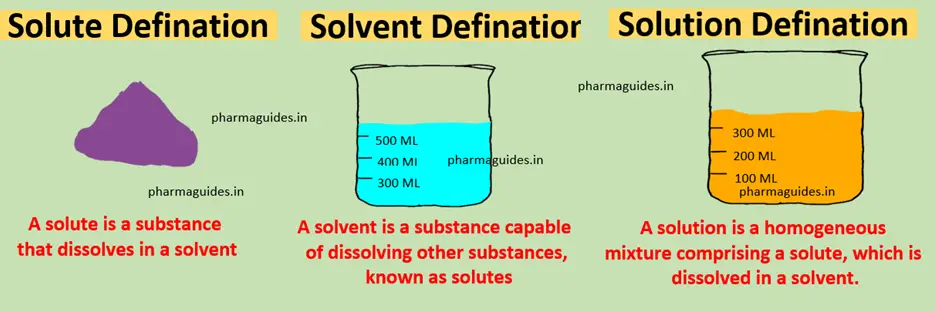
5.4 Prandtl Number: Unveiling the Secrets of Fluid Flow
Article Contents
Prandtl Number – Significance and Formula
Prandtl Number – the realm of fluid mechanics, understanding the behavior of fluids is a fundamental pursuit. From the gentle flow of a calm river to the chaotic turbulence within a jet engine, the principles governing fluid dynamics have fascinated scientists and engineers for centuries. One crucial parameter that plays a pivotal role in characterizing fluid flow is the Prandtl number. Named after the esteemed German scientist Ludwig Prandtl, this dimensionless number offers profound insights into the thermal boundary layer and the transfer of heat within a fluid.
what is Prandtl Number?
The Prandtl number (Pr) is defined as the ratio of momentum diffusivity to thermal diffusivity. It quantifies the relative importance of momentum transport (viscous forces) to thermal transport (conductive forces) in a fluid. Prandtl number is given by the formula:
Prandtl Number formula
Pr = ν / α,
where ν is the kinematic viscosity of the fluid and α is the thermal diffusivity. This dimensionless parameter is particularly significant in problems involving heat transfer and is used extensively in various fields, including aerospace engineering, meteorology, geophysics, and chemical engineering.

The concept of the Prandtl types number arises from Prandtl’s boundary layer theory, which revolutionized the understanding of fluid flow near solid boundaries. According to this theory, a thin layer called the boundary layer forms adjacent to a solid surface when a fluid flows over it. Within this boundary layer, the velocity of the fluid increases from zero at the surface to its maximum value in the mainstream flow. Simultaneously, the temperature distribution within the boundary layer changes due to heat transfer between the solid surface and the fluid.

The Prandtl type number sheds light on the nature of this thermal boundary layer. When the Prandtl number is low, such as in gases like air, the thermal diffusivity is relatively high compared to the kinematic viscosity. This implies that heat is more rapidly diffused through the fluid than momentum, resulting in a thinner thermal boundary layer. On the other hand, when the Prandtl number is high, as in many liquids, heat diffuses more slowly compared to momentum, leading to a thicker thermal boundary layer.
The Prandtl number’s influence extends beyond boundary layer theory. It affects numerous phenomena, including convection, turbulence, and energy transfer in various industrial processes. For example, in the design of heat exchangers, the Prandtl number is crucial in determining the convective heat transfer coefficient and optimizing the system’s efficiency. In meteorology, it plays a role in analyzing the thermal structure of the atmosphere, which impacts weather patterns and climate modeling.
Understanding the Prandtl the number enables engineers and scientists to make informed decisions when designing systems involving heat transfer. By manipulating the fluid properties or altering the geometry of a system, it becomes possible to enhance or control heat transfer processes. For instance, in the aerospace industry, a low Prandtl number fluid, such as liquid metal, is circulated within the leading edges of aircraft wings to mitigate the effects of high-speed air friction and prevent structural damage due to heat.
Moreover, the Prandtl the number has significant implications in the study of turbulence. Turbulent flows occur in a wide range of practical applications, from the flow of blood in arteries to the movement of ocean currents. The Prandtl number influences the transition to turbulence and the characteristics of turbulent flow, helping researchers comprehend and predict the complex behavior of fluids in such scenarios.
While the Prandtl type number is invaluable in many fluid dynamics applications, it is important to note that its value is not constant for all fluids. Different substances exhibit varying levels of momentum and thermal diffusivities, resulting in distinct Prandtl numbers. For instance, air has a Prandtl number close to 0.7
On the other hand, water has a Prantle number around 7, and oils can have even higher values. Therefore, it is crucial to consider the specific properties of the fluid under investigation when analyzing and interpreting the Prandtl type number.
In experimental studies, the Prantle number can be determined through direct measurements of the fluid’s viscosity and thermal conductivity. These values are essential inputs for numerical simulations and computational models that aim to simulate fluid flow and heat transfer phenomena accurately. By incorporating the Prandtl number into these simulations, engineers and researchers can gain a deeper understanding of the intricate details of fluid behavior and make informed decisions regarding system design and optimization.
conclusion
The Prandtl number is a powerful parameter in fluid mechanics that provides insights into the thermal boundary layer and heat transfer processes within a fluid. Its significance extends across a wide range of disciplines, including aerospace engineering, meteorology, and chemical engineering. By understanding and manipulating the Prandtl number, researchers and engineers can enhance heat transfer efficiency, optimize system designs, and gain a better understanding of complex fluid dynamics phenomena. As our knowledge and computational capabilities continue to advance, the Prandtl number remains a key tool in unlocking the secrets of fluid flow.
Read Also,
dimensionless number used in chemical engineering